
Signature Malleability Vulnerabilities in Smart Contracts
Table Of Contents
Foreword
This is third in a series of articles on vulnerabilities that smart contracts are susceptible to. You can find my articles in this topic by following the links.
This article is longer than the usual because there are a lot of pre-requisite knowledge required to understand this specific vulnerability. I did my best to explain the basics in a concise way to keep things short. Please use this article as a starting point for your research endeavor.
As always, the primary purpose for these articles is not to educate others, but to test the depth of my own understanding. That being said, I do hope that my works have even a little positive impact on others in this journey with me.
Contents
- Cryptography Basics
- Cryptography in Ethereum
- Signature Malleability Overview
- Security Risk
- Mitigation Measures
- References
Cryptography Basics
Cryptography is a branch of mathematics that is used extensively in every aspect of computer science, including blockchain technology. Lets establish the definitions of some important concepts before continuing further.
Hashing
Hashing is the process of taking in data and producing a unique output (known as hash or a digest). Even small changes in the input can significantly change the output. This property of hashing functions make it useful to detect tampering in messages. It is also practically impossible to derive the original message via the hash.
Encryption
Encryption is the art of secret writing i.e. scrambling data into an unreadable form, except for those involved in the communication. Each party has access to key(s) to achieve this. We can think of it as writing a letter in a language that only the sender and the receiver understand.
When a single key is used for both encryption and decryption purposes, It is known as symmetric encryption.
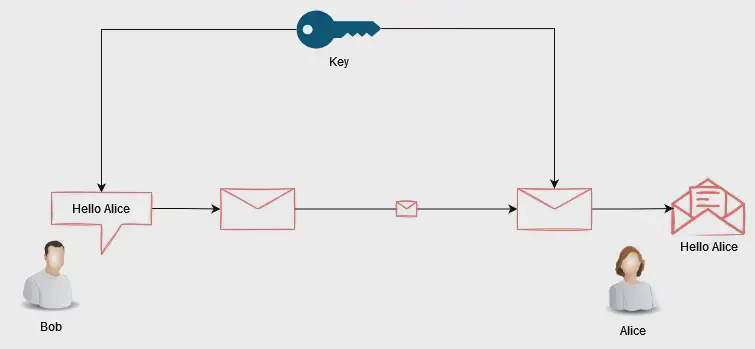
Although convenient, it is not recommended from a security perspective. Transmitting the key through public networks is not ideal as it can be intercepted and can enable bad actors to eavesdrop and modify our messages.
To remedy this**, Public key cryptography** was introduced. Public key cryptography (aka asymmetric cryptography) uses a pair of keys for encryption and decryption purposes. Specifically, the private key is used to encrypt while its associated public key is used to decrypt the data encrypted by the private key. (Although the inverse is also possible.)
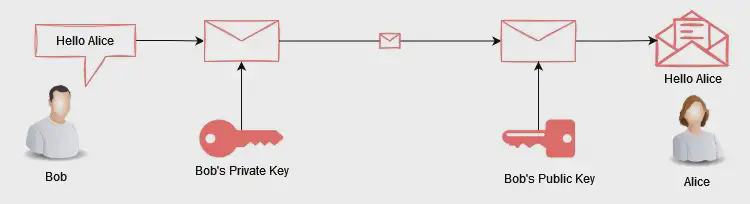
Like the name suggests, public key can be shared freely without security implications. Whereas, the private key must never be shared.
Digital Signature
The digital signature process utilizes the techniques discussed above to provide a method for receivers to verify the identity of the sender. The following illustration outlines the digital signature process.
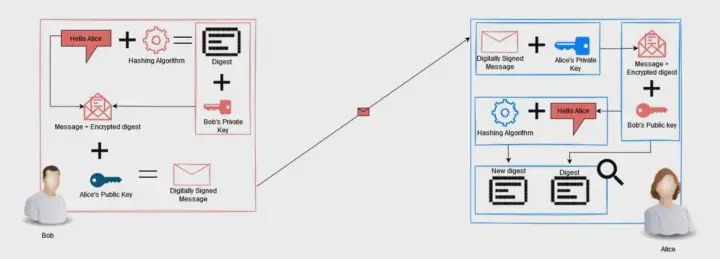
- The Message is hashed.
- The digest is encrypted with Bob’s private key.
- The encrypted hash is then concatenated with the original plain text message.
- This new combination is encrypted with Alice’s public key.
- Alice decrypts the message with her private key, and now has the plain text message and the encrypted hash.
- Alice decrypts the encrypted hash with Bob’s public key.
- Alice computes the hash of the plain text message and compares the result.
Along with confidentiality and integrity, non-repudiation is also achieved. This is because no one other than bob has access to his private key.
Cryptography in Ethereum
Ethereum’s cryptography heavily derives from Bitcoin’s Blockchain. Both blockchains use Elliptic Curve Cryptography (ECC) and Elliptic Curve Digital Signing Algorithm (ECDSA) for key generation/encryption and digital signing respectively. For hashing, Ethereum uses KECCAK-256 whereas bitcoin uses SHA-256.
Lets take a closer look at how ECC and ECDSA works before continuing. The following sections are going to be math heavy so please refer to the reference section for further research.
Elliptic Curve Cryptography Overview
Elliptic Curve Cryptography (ECC) is a public key cryptosystem, just like RSA. However, unlike RSA, ECC falls in the category of discrete logarithmic cryptosystem. For the same key length, ECC provides higher security than RSA.
Ellecptic curvrse are defined by the equation:
y² = x³+ax+b
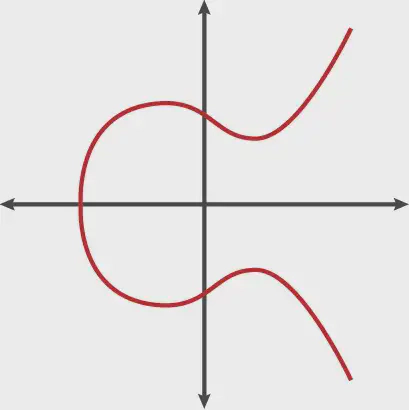
In Bitcoin’s (and Ethereum’s case), secp256k1 Elliptic curve is used, which is defined by the equation:
y² = x³+7
According to Satoshi, there wasn’t any particular reason for this. (although skeptics believe it is because secp256k1 was less likely to be backdored by the NSA).
One thing to keep in mind is the elliptic curves are symmetric about the X-axis. Another important aspect of elliptic curves that we need to know is that, any straight line intersecting the curve will intersect a maximum of three points. This will be important to understand for later sections.
Now that we have a basic understanding of elliptic curves, lets take a look at the mathematic operations we can perform.
Point Addition
Suppose we have a line that intersects the curve at three points. The sum of two intersecting points in the line segment will result in the third intersection. Mathematically;
P + Q = -R
or , P + Q + R = 0
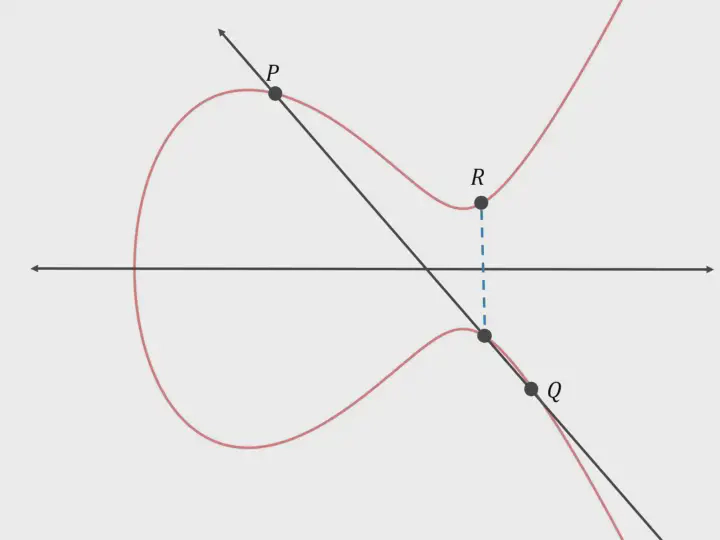
Here, the line segment intersects the curve at points P, Q and -R. The reflection of -R (i.e R) is equal to P + Q.
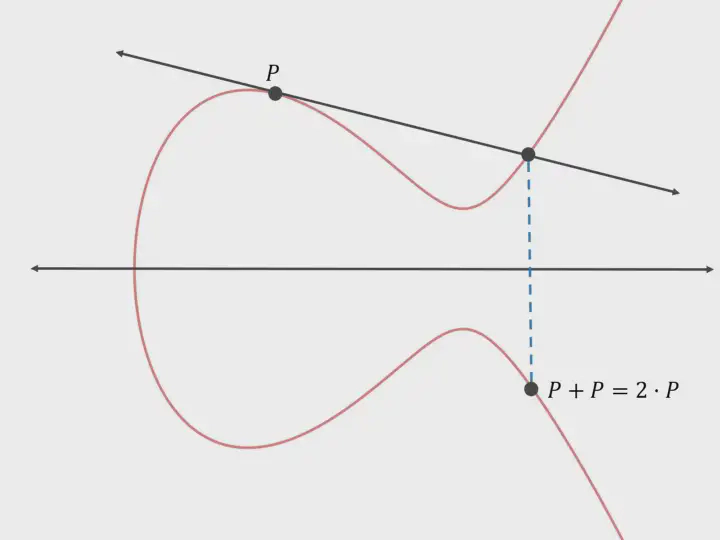
Scalar Multiplication
In mathematics, scalar multiplication refers to the multiplication a vector with a real number to get another vector. In the case of elliptic curves, we can add a point (P) to itself multiple times to get a different valid point (Q) on the curve. For this, we need to draw a tangent through the point. Mathematically,
Q = P + P + .... + P
or, Q = KP
Where, K is the number of times P was added.
Key generation
Now that we have a basic understanding behind the mathematics of elliptic curves, lets take a look at how keys are generated. The base pointer for secp256k1 Elliptic curve has the following coordinate.
For x-coordinate: 55066263022277343669578718895168534326250603453777594175500187360389116729240
y-coordinate:32670510020758816978083085130507043184471273380659243275938904335757337482424
The base pointer is scalar multiplied with a random large “K” value. This K value is our private key. The point resulting after scalar multiplication is our public key.
After considering all this, a question aeries. How is ECC suitable for cryptography?
To answer this, we must understand the concept of Trapdoor Functions. Trapdoor functions are special functions that are easy to calculate one way, but difficult to calculate in reverse, i.e it is difficult to calculate the inverse of the function. Although not impossible, it would take current supercomputers millions of years to compute.
In the case of RSA, it is trivial to find the product of two large prime numbers, however, it is significantly harder to find the prime factors of any given number. This is RSA’s trapdoor function.
In ECC, scalar product is the trap door function. Given P and K, it is easy to find Q. However, given P and Q, it is difficult to find K. This property makes it suitable for use in cryptography. This is also known as the discrete logarithm problem.
Signatures in Ethereum
In Ethereum, public key cryptography is used to determine the ownership of accounts (EOA). Specifically, the public key provides the publicly accessible account handle (the address) and Private key is used to initiate and sign transactions. The public key can be thought of as a bank account number while the private key can be thought of as the PIN.
For this reason, private keys are never transmitted or stored on Ethereum i.e. private keys never appear in messages nor are stored on-chain. This is because anyone with a copy of the private key has full control of the associated account.
ECRECOVER Overview
As mentioned above, the EVM does not store private keys on chain, thus it has no capability to sign transactions — only clients are able to do this. However, EVM does have the functionality to verify signatures. ecrecover in solidity is used to for this.
ecrecover is a pre-compiled contract available to nodes. It is used to perfrom the public key recovery function on elliptic curve cryptography, i.e. recover a public key (address) from a given signature. Lets look at the following code snip for a better understanding.
| // SPDX-License-Identifier: MIT | |
| pragma solidity ^0.8.0; | |
| contract recover { | |
| function recover(uint8 v, bytes32 r, bytes32 s, bytes32 hash) external { | |
| address signer = ecrecover(hash, v, r, s); | |
| require( signer !=address(0), "invalid ECDSA signature"); | |
| } | |
| } |
The above contract is a simple one. Here, we see that ecrecover takes four arguments. r, s and hash are of type bytes32 where as v is a uint. ecrecover will return the address (public key) of the account that was used to sign the transaction.
Security Risk
All transactions need to be signed before being included in the blockchain. As we recall, there are four required parameters for ecrecover. An attacker can modify these parameters (v, r and s) and still get a different valid signature, without having access to the private key of the original signer. This happens because elliptic curves are symmetric, and for every value of v,r and s, there will be a different set of v, r and s that have the same relationship.
This can cause problems if the signatures are being verified only at a contract level. Lets take a look at an example to understand the vulnerability better.
Suppose Alice initiates a transaction and signed it with her public key. The transaction is propagated throughout the network to be mined and included in the ledger. Among the receivers is Bob who is a menace, and he wants to perform a transaction malleability attack against Alice. He will modify the v, r and s parameters to get a valid new signature and use front running techniques (discussed here).
However, Bob cannot modify the transaction details such as the amount, receiver or the sender. No extra money will be deducted from Alice’s wallet and Bob will not get any money from Alice either. This is because all he can modify is the transaction signature that is included in the blockchain. So, what is the point then?
Lets say Alice wants to buy an NFT for 1 ether. Her wallet application will create a transaction and sign it for her. The wallet application will then look for her transaction in the blockchain to check if it was successful. But Bob has changed the signature of the transaction and this modified transaction was mined into a block and included in the ledger.
Although the payment went through, Alice’s wallet never got the confirmation, so it initiates the transaction again. This process can go on and on until all funds are exhausted. Although not confirmed, this is what is believed to have happened to Mt Gox.
Mitigation Measure
The simplest and most straight forward way of preventing signature malleability vulnerabilities would be to use the ECDS OpenZeppelin library.
It is often recommended to not reinvent the wheel and reuse code that has been tested meticulously for security flaws.
References
- https://hackernoon.com/what-is-the-math-behind-elliptic-curve-cryptography-f61b25253da3
- https://eklitzke.org/bitcoin-transaction-malleability
- https://journal0xrusowsky.substack.com/p/digital-signatures-ecrecover
- https://coders-errand.com/digital-signatures/
- https://www.youtube.com/watch?v=F3zzNa42-tQ
- https://swcregistry.io/docs/SWC-117
- https://github.com/ethereumbook/ethereumbook/blob/develop/04keys-addresses.asciidoc